Задача
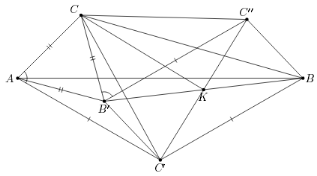
Дан треугольник ABC. На стороне AB как на основании построен во внешнюю сторону равнобедренный треугольник ABC' с углом при вершине 120°, а на стороне AC построен во внутреннюю сторону правильный треугольник ACB'. Точка K – середина отрезка BB'. Найдите углы треугольника KCC'.
Решение
Построим параллелограмм B'C'BC''. Композиция поворотов вокруг C' на 120° и C на 60° переводит B в B' и, значит, является центральной симметрией относительно K (см. рис.). При этой центральной симметрии C' переходит в C'', значит, треугольник СС'C'' – равносторонний, а так как K – середина С'C'', то CK ⊥ C'K и ∠C'CK = 30°.
Ответ
90°, 30°, 60°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет