Задача
Петя раскрасил каждую клетку квадрата 1000×1000 в один из 10 цветов. Также он придумал такой 10-клеточный многоугольник Ф, что при любом способе положить его по границам клеток на раскрашенный квадрат, все 10 накрытых им клеток будут разного цвета. Обязательно ли Ф – прямоугольник?
Решение
Заменим цвета цифрами. Первый способ. Раскрасим сначала клетки квадрата в шахматном порядке. Занумеруем все белые клетки пятью цифрами так, чтобы любой кусок длины 5 белой диагонали содержал разные цифры. Это легко сделать, так как при повороте квадрата на 45° белые клетки образуют привычную прямоугольную сетку, а куски диагоналей превращаются в прямоугольники 1×5. Аналогично занумеруем чёрные клетки пятью другими цифрами. На рисунке слева приведён пример такой раскраски и два положения Петиного многоугольника. Ясно, что в любом возможном положении он накрывает два диагональных куска длины 5 разного цвета, следовательно, содержит все 10 цифр.
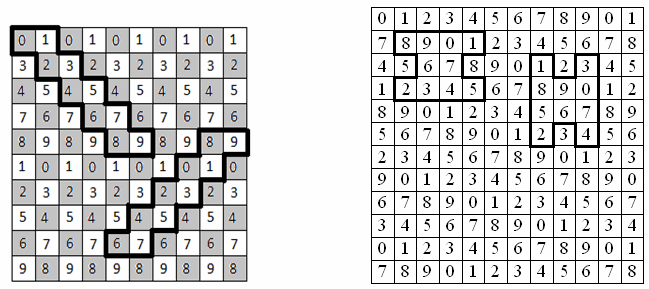
Ответ
Не обязательно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь