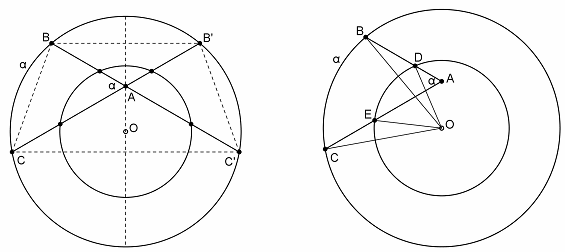
Пусть на большей окружности угол высекает дугу BC.   Первый способ. Обозначим через C' и B' вторые точки пересечения большей окружности с прямыми AB и AC соответственно (рис. слева). Сумма дуг BC и B'С' равна 2α, поэтому эти дуги равны. Значит, BB'С'C – равнобедренная трапеция или прямоугольник.

  Ось симметрии этой трапеции проходит через середины оснований, точку A пересечения диагоналей и общий центр O. Следовательно, вся картинка симметрична относительно этой оси, поэтому углы BAC и B'AС' высекают на меньшей окружности равные дуги. Сумма этих дуг равна 2α, значит, каждая из них равна α.

  Второй способ. Так как  α < 180°,  то точки O и A лежат по одну сторону от хорды BC. Значит, углы BOC и BAC одинаково ориентированы. Поэтому при повороте вокруг общего центра O, переводящем B в C, отрезок BA перейдёт в отрезок CX, где X лежит на луче CA внутри меньшей окружности. Следовательно, D перейдёт в E (это точки пересечения соответственно отрезков BA и CA с меньшей окружностью, см. рис. справа). Значит,  ⌣DE = α.

Ответ задачи отсутствует