Задача
Изначально на стол кладут 100 карточек, на каждой из которых записано по натуральному числу; при этом среди них ровно 28 карточек с нечётными числами. Затем каждую минуту проводится следующая процедура. Для каждых 12 карточек, лежащих на столе, вычисляется произведение записанных на них чисел, все эти произведения складываются, и полученное число записывается на новую карточку, которая добавляется к лежащим на столе. Можно ли выбрать исходные 100 чисел так, что для любого натурального d на столе рано или поздно появится карточка с числом, кратным 2d?
Решение
Если в некоторый момент среди чисел на карточках есть ровно k нечётных, то среди произведений чисел по 12 ровно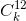 
нечётных; поэтому число на очередной добавляемой карточке будет нечётным только тогда, когда 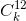нечётно (и тогда k в эту минуту увеличится на 1).
Заметим, что число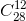 
нечётно (степени двойки, входящие в разложение чисел 28·27·...·17 и 12·11·...·1, равны). Поскольку 
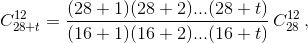наименьшее t, при котором 
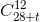чётно, равно 4. Итак, количество нечётных чисел на карточках будет расти, пока не достигнет 32 (на 4-й минуте), а после этого на карточках всегда будет ровно 32 нечётных числа.
Рассмотрим числа на карточках после n ≥ 4 минут. Пусть Tn – сумма всех произведений двенадцати из этих чисел, а En – сумма всех произведений одиннадцати из этих чисел. Число Tn+1 = Tn + EnTn = Tn(1 + En). Кроме того, 
при n ≥ 4, а число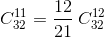 
чётно. Значит, при n ≥ 4 число 1 + En нечётно, и степень двойки, на которую делится Tn+1, равна степени двойки, на которую делится Tn.
Выберем d так, чтобы после пятой минуты ни одно из чисел на карточках (в частности, только что добавленное число T4) не делилось на 2d. Значит, и все числа T5, T6, ... не будут делиться на 2d, то есть числа, кратного 2d, никогда не появится.
Ответ
Нельзя.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь