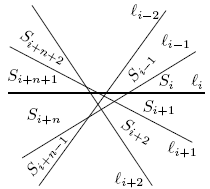
Обозначим проведённые прямые l₁, l₁, ..., l_n, упорядочив их направления по часовой стрелке (рассмотрим произвольную точку плоскости, проведём через неё прямые, параллельные нашим, занумеруем их по часовой стрелке, а потом присвоим нашим прямым те же номера, которые получили соответствующие им новые прямые).

  Среди областей, на которые наши прямые разрезали плоскость, есть 2nбесконечных кусков; обозначим их по часовой стрелкеS₁,S₂, ...,S_2nтак, что прямаяl_iразделяет кускиS_iиS_i+1, а также кускиS_i+nиS_i+n+1(мы считаем, что  S_2n+1=S₁).   Сначала во все области (конечные и бесконечные) поставим по 1. Для каждой прямойl_iобозначим через 2Σ_iразность сумм чисел слева и справа отl_i(мы считаем, что кускиS_iиS_i+n+1лежат слева отl_i). Если  Σ_i> 0,  то прибавим по Σ_iк числам, стоящих вS_i+1иS_i+n. При этом все числа Σ_jпри  j ≠ i  не изменились, поскольку областиS_iиS_i+n+1лежат по разные стороны относительно каждой прямой, кромеl_i. Число же Σ_iстало равно нулю. Если  Σ_i< 0,  то вычтем Σ_iиз чисел, стоящих вS_iиS_i+n+1; при этом Σ_iстанет равна 0, а остальные Σ_jне изменятся.   Такими операциями мы последовательно сделаем каждое Σ_iравным нулю, не меняя остальных.

Ответ задачи отсутствует