Задача
Олег нарисовал пустую таблицу 50×50 и написал сверху от каждого столбца и слева от каждой строки по числу. Оказалось, что все 100 написанных чисел различны, причём 50 из них рациональные, а остальные 50 – иррациональные. Затем в каждую клетку таблицы он записал произведение чисел, написанных около её строки и её столбца ("таблица умножения"). Какое наибольшее количество произведений в этой таблице могли оказаться рациональными числами?
Решение
Оценка. Предположим, что среди рациональных чисел есть 0 и он выписан у верхней стороны таблицы. Пусть вдоль левой стороны таблицы выписано x иррациональных и 50 – x рациональных чисел. Тогда вдоль верхней стороны выписаны 50 – x иррациональных и x рациональных чисел. Заметим, что произведение ненулевого рационального и иррационального чисел иррационально. Значит, в таблице есть как минимум x(x – 1) + (50 – x)2 = 2x2 – 101x + 502 иррациональных чисел. Вершина параболы y = 2x2 – 101x + 502 находится в точке 25,25, поэтому минимальное значение этой функции в целой точке достигается при x = 25 и равно 25·24 + 252 = 1225.
Если же 0 заменить ненулевым рациональным числом, то количество иррациональных чисел может только увеличиться. Поэтому в таблице в любом случае не более 2500 – 1225 = 1275 рациональных чисел.
Пример, когда рациональных чисел 1275. Вдоль левой стороны поставим числа 1, 2, ..., 24, 25,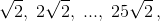 
а вдоль верхней – числа 0, 26, 27, ..., 49, 
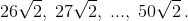Тогда иррациональными будут только 25·24 + 252 = 1225 произведений ненулевого рационального и иррационального чисел.
Ответ
1275 произведений.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь