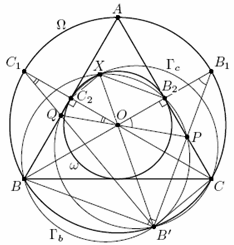
Пусть B₂ и C₂ – точки касания ω с AC и AB соответственно, а B₁ и C₁ – точки, диаметрально противоположные точкам B и C (см. рис.). Тогда точки B₁ и C₁ симметричны O относительно сторон AC и AB соответственно, откуда  ∠OB₁P = ∠B₁OP,  ∠OC₁Q = ∠C₁OQ,

∠OB₁P + ∠OC₁Q = 180° – ∠B₂OC₂ = ∠A = 60°.

  Пусть лучB₁Pпересекает Ω в точкеB'. Тогда  ∠B'C₁C= ∠B'AC= 60° – ∠BAB'= 60° – ∠BB₁B'= 60° – ∠OB₁P= ∠OC₁Q= ∠CC₁Q,  значит, точкаQлежит на прямойC₁B'.   ∠PB'B= ∠B₁B'B= 90°,  то естьB'лежит на Г_b. АналогичноB'лежит на Г_c. Итак, Г_bи Г_cпересекаются в точкеB', лежащей на Ω.   Заметим, что точкиB₂иC₂лежат на Г_bи Г_cсоответственно. Пусть продолжение отрезкаB'Oза точкуOпересекает ω в точкеX. Тогда OB·OB₂=OB'·OX = OC·OC₂.  Первое из этих равенств означает, что точкиB, B₂,B'иXлежат на одной окружности, то естьXлежит на Г_b. АналогичноXлежит на Г_c. Значит,Xи является второй точкой пересечения Г_bи Г_c, лежащей на ω.

Ответ задачи отсутствует