Задачи и олимпиады по математике

Задача

В прямоугольнике ABCD на диагонали AC отмечена точка K так, что CK = BC. На стороне ВС отмечена точка М так, что КМ = СМ. Докажите, что АK + ВМ = СМ.

Решение

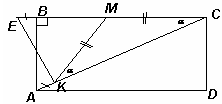
На продолжении стороны BC за точку В отметим такую точку Е, что BЕ = AK, тогда CЕ = СB + BЕ = СK + KА = СА (см. рис.).

ТреугольникиЕKCиABCравны по двум сторонам и общему углу между ними. Следовательно, ∠ЕKC= ∠ABC= 90°. Пусть ∠KCM= ∠MKC= α, тогда ∠MKE= 90° – α = ∠MEK, значит, МЕ = MK = МС. Таким образом, АK + ВМ = ВЕ + ВМ = МЕ = СМ.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления