Задача
Докажите, что можно найти бесконечно много таких пар целых чисел, что в десятичной записи каждого числа все цифры не меньше 7 и произведение чисел каждой пары – тоже число, где все цифры не меньше 7.
Решение
Рассмотрим произведение 3n-значных чисел 887887...887887·999999…999877. Заметим сначала, что 887·123 = 109101. Поэтому 887887…887887·123 = 109210210...210101 (3n + 3 знака).
Наконец, 887887...887887·999999…999877 = 887887...887887·(103n – 123) = 887887...887887·103n – 109210210...210101 =
= 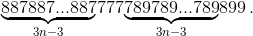
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет