Задача
По краю многоугольного стола ползут два муравья. Все стороны стола длиннее 1 м, а расстояние между муравьями всегда ровно 10 см. Сначала оба муравья находятся на одной из сторон стола.
a) Пусть стол выпуклый. Всегда ли муравьи смогут проползти по краю стола так, чтобы в каждой точке края побывал каждый из муравьев?
б) Пусть стол не обязательно выпуклый. Всегда ли муравьи смогут проползти по краю стола так, чтобы на краю не осталось точек, в которых не побывал ни один из муравьев?
Решение
a) Рассмотрим стол в виде равнобедренного треугольника с горизонтальным основанием и высотой, меньшей 10 см. Муравьи не могут оказаться на одной вертикали: тогда бы они оказались слишком близко друг к другу. Поэтому правый муравей всегда останется правее левого и, значит, не сможет попасть в левую вершину. б) Возьмём равнобедренный треугольник ABC с горизонтальным основанием AC меньше 10 см и на его оси симметрии отметим точку D так, чтобы и BD было меньше 10 см. Изготовим стол в форме невыпуклого четырёхугольника ABCD (см. рис.). Аналогично a) муравьи не могут оказаться на одной горизонтали, поэтому один из них всегда будет находиться выше другого. Верхний не может пройти через точки A и C, а нижний – через B и D (все точки выше вершины D ближе 10 см к ней). Значит, каждый из муравьев может гулять только по двум соседним сторонам (включая исходную), поэтому на "противоположную" сторону ни один из них не попадёт.
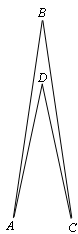
Ответ
Не всегда.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь