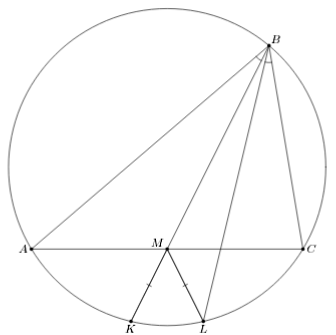
Пусть K – точка пересечения медианы BM и симедианы с описанной окружностью. Так как  ∠ABK = ∠CBL,  точки K и L равноудалены от точки M стороны AC (см. рис.). Отсюда получаем следующее построение.

  Продолжим отрезок отBдо центра тяжести на половину его длины, построив тем самым точкуM. Проведём через точкуLокружность с центромMи найдём точкуKеё пересечения сBM, лежащую вне лучаMB. Построим окружностьBKLи найдём точкиA, Cеё пересечения с прямой, проходящей черезMпараллельноKL. ТреугольникABCискомый.

Ответ задачи отсутствует