Задача
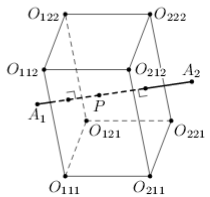
В пространстве даны три отрезка A1A2, B1B2 и C1C2, не лежащие в одной плоскости и пересекающиеся в одной точке P. Обозначим через Oijk центр сферы, проходящей через точки Ai, Bj, Ck и P. Докажите, что прямые O111O222, O112O221, O121O212 и O211O122 пересекаются в одной точке.
Решение
Для любого отрезка XY серединным перпендикуляром к этому отрезку назовём плоскость, перпендикулярную ему и проходящую через его середину, то есть геометрическое место точек, равноудалённых от X и Y.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет