Решение 1:   Представим себе, что доминошки (прямоугольники 1×2) ещё не вырезаны, и будем вырезать их по одной. В каждый момент процесса назовём ценой ещё не вырезанной клетки число её невырезанных соседей по стороне, уменьшенное на 2 (например, цена неугловой клетки, лежащей на границе квадрата, изначально равна 1). Тогда исходная цена каждой клетки есть  2 – t,  где t – количество отрезков периметра квадрата, находящихся на границе этой клетки. Значит, исходная суммарная цена всех клеток равна  2·100² – 400 = 19600.

  Проследим, как изменяется суммарная цена S всех невырезанных клеток после вырезания доминошки. При этом выкидываются две клетки (сумма цен которых не превосходит  2 + 2 = 4),  а также уменьшаются на 1 цены клеток, граничащих с доминошкой (а их не больше шести). Поэтому после вырезания доминошки S уменьшается не более, чем на 10.

  Итак, после вырезания 1950 доминошек S будет не меньше, чем  19600 – 1950·10 = 100.  Поэтому найдётся невырезанная клетка k, цена которой положительна. Это значит, что у k не менее трёх невырезанных соседей. Тогда k вместе с этими тремя соседями образует требуемую фигурку.

Решение 2:   Назовём требуемую фигурку T-тетрамино.   Разобьём наш квадрат на фигурки (см. рис.). Нетрудно подсчитать, что вне "полных" крестов окажется ровно  4·100 = 400  клеток, из которых 320 будут находиться в T-тетрамино разбиения. Итого, в разбиении есть  (100² – 400) : 5 = 1920  полных крестов и ещё 80 T-тетрамино.

  Рассмотрим теперь, куда попадают клетки вырезанных доминошек. Предположим, что из каждого полного креста было вырезано хотя бы по две клетки, а из каждого T-тетрамино разбиения – хотя бы одна. Тогда общее число вырезанных клеток было бы не меньше чем  1920·2 + 80 = 2·1960,  что неверно.   Значит, либо из некоторого T-тетрамино не вырезано ни одной клетки, либо из некоторого креста вырезано не более одной клетки. В первом случае мы уже нашли T-тетрамино, которое можно вырезать. Во втором же случае, если из креста и вырезана одна клетка, то она не может быть центральной (иначе вторая клетка той же доминошки также лежала бы в кресте). Значит, даже если клетка креста вырезана, остаток его как раз и является T-тетрамино. В обоих случаях мы добились требуемого.

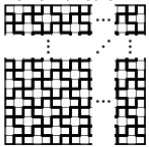
Ответ задачи отсутствует