Задача
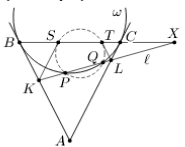
Окружность ω касается сторон угла BAC в точках B и C. Прямая l пересекает отрезки AB и AC в точках K и L соответственно. Окружность ω пересекает l в точках P и Q. Точки S и T выбраны на отрезке BC так, что KS || AC и LT || AB. Докажите, что точки P, Q, S и T лежат на одной окружности.
Решение
Если l || BC, утверждение очевидно в силу симметрии относительно серединного перпендикуляра к BC.
Пусть прямые l и BC пересекаются в точке X (см. рис.). Из параллельности получаем XB : XT = XK : XL = XS : XC, откуда XT·XS = XB·XC = XP·XQ. Следовательно, точки P, Q, S и T лежат на одной окружности.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет