а) Пусть A₁A₂...A₁₄ – правильный 14-угольник (см. рис.). Отметим шесть его вершин: A₁, A₂, A₄, A₈, A₉, A₁₁. Ясно, что если некоторые два отрезка с концами в вершинах этого многоугольника параллельны, то между ними с двух сторон лежит равное число сторон 14-угольника. Из отрезков с концами в отмеченных шести вершинах этим свойством обладают только пары отрезков A₁A₂ и A₈A₉, A₂A₄ и A₉A₁₁, A₁A₄ и A₈A₁₁, A₄A₈ и A₁A₁₁, A₄A₉ и A₂A₁₁, A₁A₉ и A₂A₈. Перечисленные пары отрезков являются сторонами трёх параллелограммов, вписанных в окружность, то есть прямоугольников.

  б) Докажем, что какие бы семь вершин правильного 14-угольника ни были отмечены, всегда найдётся трапеция с вершинами в отмеченных точках. Проведём прямые через всевозможные пары вершин правильного 14-угольника. Покажем, что среди этих прямых можно выбрать 14 попарно не параллельных, а среди любых 15 прямых хотя бы две будут параллельны (если прямые параллельны, то будем далее говорить, что они имеют одно направление). В самом деле, прямые A₁A₂, A₃A₁₄, ..., A₈A₉ имеют одно направление. Прямые A₁A₁₄, A₂A₁₃, ..., A₇A₈ также имеют одно направление, отличное от уже рассмотренного, поскольку каждая из них получается из соответствующей прямой первого направления поворотом на угол ^π/₇ вокруг центра 14-угольника. Поворачивая эти прямые на тот же угол далее, получим еще пять новых направлений. Рассмотрим теперь прямые A₃A₁, A₄A₁₄, ..., A₈A₁₀. Все они имеют одно направление, отличное от семи, указанных выше. Шестью последовательными поворотами этих прямых на угол ^π/₇ вокруг центра 14-угольника получим еще шесть новых направлений прямых, проходящих через вершины правильного 14-угольника. Остаётся заметить, что любая прямая, содержащая отрезок с концами в вершинах правильного 14-угольника, имеет одно из перечисленных 14 направлений, а именно, если между концами отрезка лежит чётное число вершин, то одно из первых семи направлений, а если нечётное, то одно из последних семи направлений.   Соединим все отмеченные вершины отрезками; их число равно  7·6 : 2 = 21.  Если некоторые три отрезка имеют одно направление, то некоторые два из них являются основаниями трапеции. В самом деле, если параллелограмм вписан в окружность, то он прямоугольник, причём его противоположные стороны стягивают одинаковое число сторон многоугольника. Следовательно, если вершины каких-либо двух из трёх отрезков данного направления лежат в вершинах такого прямоугольника, то концы любого из этих двух отрезков и третьего отрезка лежат в вершинах трапеции.

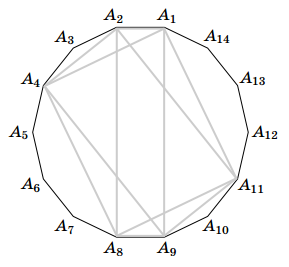
  Пусть теперь для каждого из 14 направлений имеется не более двух отрезков из 21 проведённых. Это означает, что существуют не менее семи направлений, для каждого из которых есть ровно два параллельных отрезка с концами в отмеченных точках. Рассмотрим любое направление, для которого есть два таких отрезка. Обозначим их AB и CD. Если они не являются основаниями трапеции, то это стороны прямоугольника, поэтому отрезки AC и BD параллельны и принадлежат перпендикулярному направлению. Следовательно, все направления, для которых имеются два отрезка, распадаются на пары взаимно перпендикулярных, а значит, число направлений, для каждого из которых есть ровно два параллельных отрезка с концами в отмеченных точках, не меньше восьми, а соответствующие пары взаимно перпендикулярных отрезков являются сторонами не менее четырёх различных прямоугольников с вершинами в отмеченных точках. Поскольку все вершины каждого прямоугольника разбиваются на пары диаметрально противоположных, а среди семи отмеченных точек хотя бы одна такова, что диаметрально противоположная ей точка не отмечена, получаем, что вершины прямоугольников могут располагаться не более чем в шести из отмеченных точек. Но может существовать не более трёх различных прямоугольников с вершинами в шести данных точках окружности. Противоречие.

а) Можно;  б) нельзя.