Решение 1:   Наиболее простой пример получается периодическим повторением расстановки, показанной на рисунке.

  Если соседи чёрной клетки по горизонтали по модулю равны 1, то их произведение равно –1, а произведение её соседей по вертикали равно –2. Если же соседи чёрной клетки по вертикали по модулю равны 1, то их произведение равно 1, а произведение ее соседей по горизонтали равно 2. Для каждой чёрной клетки выполняется одно из этих условий, а значит, подсчитанное для каждой чёрной клетки число равно единице.

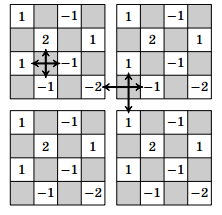
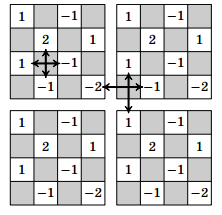
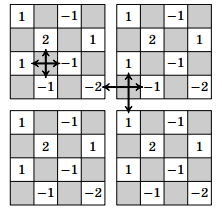
Решение 2:   В двух соседних вертикалях ставим число  x₀ = 1,  в соседних с ними  x₁ = 2,  затем  x₂ = 5  и т.д. по правилу  x_n = F_{2n+ 1},  где F_2n+1 – это (2n+1)-е число Фибоначчи. Часть этой расстановки в квадрате 6×6 показана на рисунке.

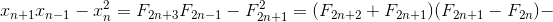  Тогда условие для каждой черной клетки будет выполнено: если черная клетка стоит в вертикали с числамиx_n, то ей соответствует число –  (см. задачу160564).

Решение 3:   Этот способ замечателен тем, что на доске встречаются все натуральные числа и расстановка задается явной формулой.

  Введём на плоскости систему координат, начало которой – в центре белой клетки, оси параллельны сторонам клеток, а единичный отрезок равен стороне клетки. Поставим в белую клетку с центром в точке  (x, y)  число  f(x, y),  равное  |y| + 1,  если  |x| ≤ |y|,  и  ½ (x² – y²) + |x| + 1,  если  |x| > |y|.

  В частности, для квадрата 9×9 с центром в начале координат получится расстановка на рисунке ниже. На каждой диагонали мы видим две арифметические прогрессии.

  Докажем, что данная расстановка удовлетворяет условию. Сразу видно, что все числа  f(x, y)  положительны. Координаты  (x, y)  центра любой белой клетки – целые числа одинаковой чётности, поэтому все числа  f(x, y)  – целые.   Пусть  (x, y)  – координаты центра чёрной клетки. Это целые числа разной чётности. Так как расстановка симметрична, то можно считать, что x, y≥ 0.  Тогда в клетке  (x, y)  стоит число  g(x, y) =f(x– 1,y)f(x+ 1,y) –f(x, y+ 1)f(x, y– 1).  Возможны два случая.   1)  x < y.  Тогда  g(x, y) = (y+ 1)² – (y+ 1 + 1)(y– 1 + 1) = (y+ 1)² – ((y+ 1)² – 1) = 1.  Мы не пишем знак модуля, так как из условий  y > x≥ 0  следует, что  y≥ 1.   2)  x > y.  Пользуясь несколько раз тождеством  (a + b)(a – b) =a² –b²,  снова получим: g(x, y) = (½ ((x– 1)² –y²) +x– 1 + 1)(½ ((x+ 1)² –y²) +x+ 1 + 1) – (½ (x² – (y+ 1)²) +x+ 1)(½ (x² – (y– 1)²) +x+ 1) =     = (½ (x² + 1 –y²) +x+ 1)² – (x+ 1)² – (½ (x² –y² – 1) +x+ 1)² +y²= (x² –y² + 2x+ 2)·1 – (x+ 1)² +y² = 1.   Итак, для каждой чёрной клетки нужное условие выполнено.

Могут.