Задачи и олимпиады по математике

Задача

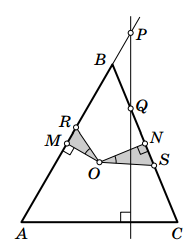
Точка O – центр описанной окружности остроугольного треугольника ABC. Прямая, перпендикулярная стороне AC, пересекает сторону BC и прямую AB в точках Q и P соответственно. Докажите, что точки B, O и середины отрезков AP и CQ лежат на одной окружности.

Решение

Пусть M, N, R, S – середины отрезков AB, BC, AP и CQ соответственно. Заметим, что ∠OMB = ∠ONB = 90°, ∠OMN = 90° – ∠NMB = 90° – ∠A = ∠BPQ.

Аналогично ∠ONM= ∠BQP. Следовательно, треугольникиOMNиBPQподобны. Значит, OM:BP = ON:BQ. Имеем MR = AR– AM = ½AP– ½AB= ½BP. Аналогично NS= ½BQ. Таким образом, OM:MR = ON:NS, и треугольникиOMRиONSподобны. Поэтому ∠ORM= ∠OSN, значит, ∠ORB+ ∠OSB= 180°, и четырёхугольникORBS– вписанный.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления