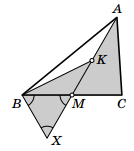
Решение 1:На продолжении медианы AM за точку M отметим такую точку X, что  MX = BM  (рис. слева). Заметим, что треугольник BMX – равносторонний. Треугольники BXK и CMA равны по двум сторонам и углу между ними.

                       

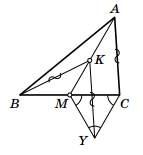
Решение 2:Отразим вершину B относительно прямой AM; получим точку Y (рис. в центре). Заметим, что  BM = MY  и   ∠BMY = 120°,  откуда видно, что треугольник CMY – равносторонний. Отрезки AK и CY параллельны и равны; следовательно, AKYC – параллелограмм. Значит,  AC = YK,  а отрезки YK и BK равны из симметрии относительно AM.

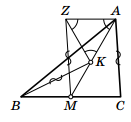
Решение 3:Отметим такую точку Z, что MCAZ – параллелограмм. Несложно видеть, что AKZ – равносторонний треугольник. Значит, ZKMB   равнобедренная трапеция:  BM = KZ,  ∠BMK = ∠MKZ = 120°.  Отрезки AC и MZ равны как стороны параллелограмма, отрезки MZ и BK – как диагонали равнобедренной трапеции.

Ответ задачи отсутствует