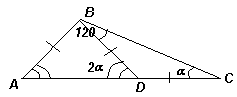
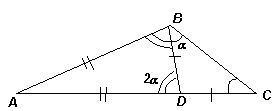
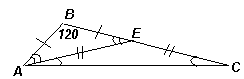
Пусть в треугольникеАВС  ∠В= 120°.   Разрез, указанный в условии задачи, должен проходить через вершину треугольника (иначе при разбиении не получится два треугольника). При этом он может проходить как через вершинуВ, так и через другую вершину.   В первом случае (BD– линия разреза), хотя бы один из образовавшихся треугольников, например, треугольникBDCне будет остроугольным, поэтомуВС– его основание. Тогда  ∠DВС= ∠DСВ= α,  ∠ВDA= 2α  – внешний для треугольникаBDC. При этом в треугольникеABDсторонаABоснованием быть не может (иначе из равенства  DA = DB = DC  будет следовать, что  ∠В= 90°,  что противоречит условию). Следовательно, его основанием является либоAD, либоBD.

  ЕслиAD – основание, то  AB = DB  (рис. слева). Тогда  ∠А= ∠ВDA= 2α.  Из треугольникаАВСполучим  2α + α = 60°,  α = 20°.  Таким образом, ∠C= 20°,  ∠А= 40°.   ЕслиBD– основание, то  AB = AD  (рис. справа). Тогда  ∠АВD= ∠ВDA= 2α.  Значит,  ∠В= 3α,  α = 40°,  то есть  ∠C= 40°.   Во втором случае линия разреза должна пройти через вершину большего из двух острых углов (AE– линия разреза, см. рис.). Тогда оба образовавшихся треугольника будут тупоугольными. При этом  АВ = ВЕ  и  АЕ =  ЕС. Следовательно, ∠ВАЕ= ∠ВЕА= ½ (180° – ∠В) = 30°,  а ∠ЕАС= ∠ЕСА= ½ ∠ВЕА= 15°.

  Таким образом,  ∠C= 15°,  ∠А= 45°.

40° и 20° или 45° и 15°.