Задачи и олимпиады по математике

Задача

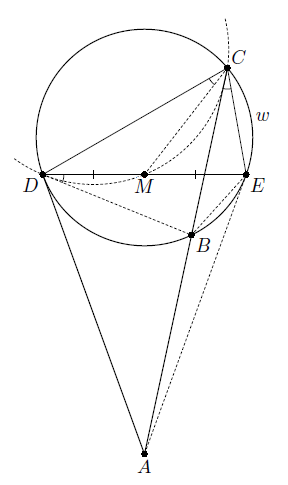
Из точки A к окружности ω проведена касательная AD и произвольная секущая, пересекающая окружность в точках B и C (B лежит между точками A и C). Докажите, что окружность, проходящая через точки C и D и касающаяся прямой BD, проходит через фиксированную точку (отличную от D).

Решение

Проведём из точки A вторую касательную AE к окружности ω (см. рис.). Пусть M – середина отрезка DE.

Докажем, что окружность, проходящая через точкиCиDи касающаяся прямойBD, проходит через точкуMили, что то же самое, описанная окружность треугольникаDCMкасается прямойBD. Рассмотрим треугольникDCE. В немCM– медиана, аCA–симедиана(см. задачу156983). Следовательно, ∠DCM= ∠BCE= ∠BDE. Значит,BD– касательная к описанной окружности треугольникаDCM.

Ответ

Ответ задачи отсутствует

Задача

Решение

Ответ

Подтверждение удаления