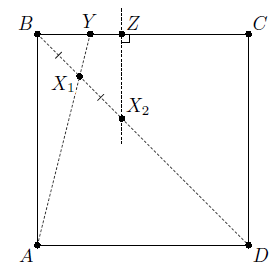
Заметим, что мы можем поделить пополам любой отрезок, совместив его концы. Кроме того, можно перегнуть бумагу по прямой, проходящей через данную точку, перпендикулярно данной прямой. Иными словами, мы умеем строить середины отрезков и перпендикуляр к данной прямой, проходящий через данную точку. Воспользуемся при решении задачи этими построениями и тем, что  2016 = 32·63.

  Перегнём квадрат ABCD по диагонали BD, а затем шесть раз по перпендикулярным ей прямым так, что эта диагональ разделится на 64 равных части. Пусть X₁ и X₂ лежат на диагонали BD, причём  BX₁ = X₁X₂ = ¹/₆₄ BD  (см. рис.).

  Пусть прямаяAX₁пересекаетBCв точкеY. Тогда  BY:BC = BY:AD = BX₁:X₁D= 1 : 63,  то есть  BY= 32.  Рассмотрев точкуZ– проекциюX₂наBC, получим, что  BZ:BC=BX₂:BD= 1 : 32,  то есть  BZ= 63.  Поэтому, перегнув по прямымAX₁иX₂Z, а затем по прямой, проходящей черезYи перпендикулярнойBC, получим отрезок длины  2BY – BZ= 1.

Можно.