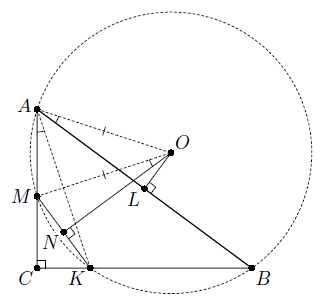
Пусть ABC – данный прямоугольный треугольник, точки L и N – основания перпендикуляров, опущенных из точки O на прямые AB и MK соответственно (см. рис.). Докажем, что треугольники MON и OAL равны, откуда и будет следовать утверждение задачи. Заметим, что гипотенузы у них равны, как радиусы, то есть достаточно доказать равенство углов MON и OAL.

  Пусть  ∠MON= α,  тогда центральный уголMOKравен 2α, а соответствующий ему вписанный уголMAKравен α. Далее, вписанный в окружность уголAKBравен  90° + α  как внешний угол треугольникаCAK. Следовательно, центральный уголAOB, опирающийся на меньшую дугуAB, равен 80° – 2α,  то есть  ∠OAL= ∠OAB= α,  что и требовалось.

Ответ задачи отсутствует