Заметим, что 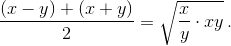    С помощью перебора найдём на доске пару чисел  a < b,  чьё среднее арифметическое равно среднему геометрическому оставшейся пары чисел c и d. Ниже мы докажем, что такое разбиение единственно (с точностью до перестановки равных чисел), поэтому  a = x – y,  b = x + y,  откуда  x = ½ (a + b),  y = ½ (b – a).

  Докажем единственность. Если в равенстве     поменять местами два неравных числа из разных частей, то равенство нарушится: ведь одна из частей увеличится, а другая – уменьшится. Поменять пары целиком тоже нельзя: отрицательное число не может стоять под корнем, а если все числа неотрицательны, то 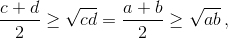    и равенство достигается, только когда все четыре числа равны, что невозможно:

x + y > x – y.

Ответ задачи отсутствует