Задача
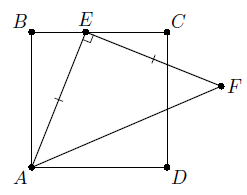
Квадрат ABCD и равнобедренный прямоугольный треугольник AEF (∠AEF = 90°) расположены так, что точка E лежит на отрезке BC (см. рисунок). Найдите угол DCF.
Решение
Решение 1:Пусть P – основание перпендикуляра, опущенного из точки F на прямую BC (рис. слева). Так как ∠FEP = 90° – ∠BEA = ∠EAB, то прямоугольные треугольники FEP и EAB равны (по гипотенузе и острому углу). Следовательно, PF = BE. Кроме того, BE = BC – CE = AB – CE = EP – CE = PC. Таким образом, PF = PC, то есть треугольник CPF прямоугольный и равнобедренный. Значит, ∠FCP = 45°, тогда и ∠DCF = 45°.
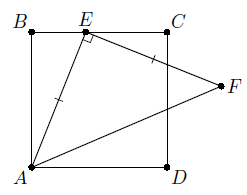
Решение 2:Проведём диагональ AC. Так как ∠ECA = ∠EFA = 45°, то четырёхугольник ECFA – вписанный (рис. справа). Значит, ∠ACF = ∠AEF = 90°. Следовательно, ∠DCF = ∠ACF – ∠ACD = 45°.
Ответ
45°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь