Задача
В треугольник ABC вписана окружность с центром O. На стороне AB выбрана точка P, а на продолжении стороны AC за точку C – точка Q так, что отрезок PQ касается окружности. Докажите, что ∠BOP = ∠COQ.
Решение
Решение 1:Центр окружности, вписанной в угол, лежит на его биссектрисе. Применяя для треугольника BOP теорему о внешнем угле (см. рис.), получим
∠BOP = ∠APO – ∠ABO = ½ ∠APQ – ½ ∠B. Аналогично, ∠COQ = ∠ACO – ∠AQO = ½ ∠C – ½ ∠AQP. Осталось убедиться, что
∠APQ – ∠B = ∠C – ∠AQP. Это равенство равносильно тому, что ∠APQ + ∠AQP = ∠B + ∠C, которое, очевидно, выполняется, так как каждая его часть равна 180° – ∠A.
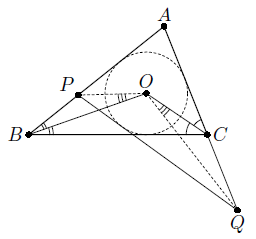
Решение 2:Заметим, что для треугольника PAQ данная окружность также является вписанной (см. рис.). Значит, O – точка пересечения биссектрис как в треугольнике BAC, так и в треугольнике PAQ. Следовательно, ∠BOC = 90° + ½ ∠BAC = ∠POQ (см. задачу 155448). Следовательно,
∠BOP = ∠POQ – ∠BOQ = ∠BOC – ∠BOQ = ∠COQ.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь