Задача
Внутри равностороннего треугольника ABC отмечена произвольная точка M. Докажите, что можно выбрать на стороне AB точку C1, на стороне BC – точку A1, а на стороне AC – точку B1 таким образом, чтобы длины сторон треугольника A1B1C1 были равны отрезкам MA, MB и MC.
Решение
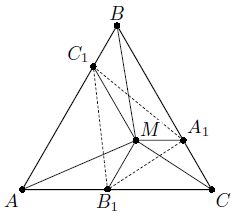
Отметим на стороне AB точку C1, на стороне BC точку A1, а на стороне AC точку B1 таким образом, что MC1 || BC, MA1 || AC, MB1 || AB (см. рис.). Тогда отрезки MA1, MB1 и MC1 разобьют данный треугольник на три трапеции. Из параллельности следует, что каждый угол при большем основании этих трапеций равен 60°, поэтому эти трапеции равнобокие. Следовательно, в каждой трапеции диагонали равны: B1C1 = MA, A1C1 = MB, A1B1 = MC.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь