Задача
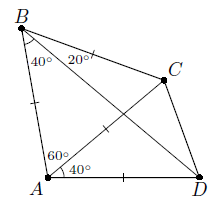
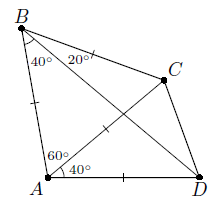
ABCD – выпуклый четырёхугольник. Известно, что ∠CAD = ∠DBA = 40°, ∠CAB = 60°, ∠CBD = 20°. Найдите угол CDB.
Решение
Так как ∠CAB = 60°, ∠ABC = ∠ABD + ∠DBC = 60°, то треугольник ABC – равносторонний (рис. слева). Далее можно рассуждать по-разному. Первый способ. В треугольнике ABD ∠ABD = 40°, ∠BAD = ∠BAC + ∠CAD = 100°, значит, ∠BDA = 180° – (40° + 100°) = 40°. Следовательно, этот треугольник – равнобедренный (рис. слева). Таким образом, AB = BC = CA = AD, поэтому треугольник CAD – также равнобедренный. Значит,
∠ADC = ∠ACD = ½ (180° – ∠CAD) = 70°, ∠CDB = ∠CDA – ∠BDA = 70° – 40° = 30°.
Ответ
30°.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет