Задача
Четырёхугольник АВСD вписан в окружность, I – центр вписанной окружности треугольника ABD.
Найдите наименьшее значение BD, если AI = BC = CD = 2.
Решение
Из условия следует равенство дуг BC и CD, значит, биссектриса AI угла ВАD пересекает окружность в точке С (см. рисунки). По лемме о трезубце
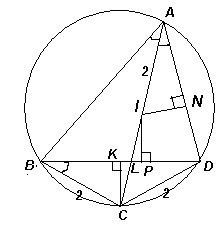
СI = CB = CD = 2. Далее можно рассуждать по-разному. Первый способ. Пусть K и N – основания перпендикуляров, опущенных из точек C и I на BD и AD соответственно (рис. слева), тогда из равенства прямоугольных треугольников BKC и ANI следует, что CK = IN. Перпендикуляр IP к диагонали BD также равен IN (это радиусы вписанной окружности треугольника ABD), поэтому BD пересекает отрезок CI в его середине L. Таким образом, CL = IL = 1.
По теореме о произведении отрезков хорд BL·
DL = AL·CL. Пусть BL = x, DL = y, тогда xy = 3. Из неравенства Коши следует, что наименьшее значения суммы x + y достигается, если x = y = 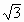 .
Следовательно, значение BD = 2
.
Следовательно, значение BD = 2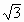 – наименьшее из возможных.
– наименьшее из возможных.
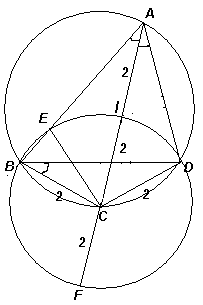
Без ограничения общности можно считать, что AB ≥ AD. Проведём окружность с центром С и радиусом 2, которая пересечёт сторону АВ в точке Е (рис. справа). Биссектриса АС угла ВАD является её осью симметрии и осью симметрии угла, значит, точки E и D симметричны относительно АС. Следовательно, АЕ = AD.
По теореме о произведении отрезков секущих АЕ· АВ = AI·AF (IF – диаметр построенной окружности). Следовательно, АD·АВ = 2· 6 = 12.
По неравенству Коши BD = ½ (AB + AD) ≥ 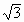 = 2
= 2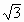 . Равенство достигается, если AB = AD.
. Равенство достигается, если AB = AD.
Ответ
2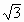 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь