Решение 1:   На описанной окружности Ω треугольника ABC отметим точку X так, что  ∠XA₁C = ∠CA₁A.  Тогда X симметрична второй точке пересечения прямой AA₁ с Ω относительно серединного перпендикуляра к BC, так что  A₁X·A₁A = A₁B·A₁C = A₁C².  Отсюда следует, что треугольники XA₁C и CA₁A подобны.

  Пусть T – середина AA₁. Тогда XC₂ и CT – соответственные медианы в подобных треугольниках, откуда  ∠CXC₂ = ∠ACT (рис. слева). С другой стороны, CTC₂C₃ – параллелограмм, так что  ∠CC₃C₂ = ∠ACT = ∠CXC₂.  Это значит, что X лежит на описанной окружности треугольника CC₂C₃.

  Аналогично X лежит на описанной окружности треугольника BB₂B₃. Поэтому X и есть искомая точка.

             

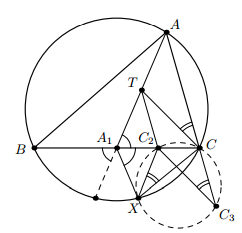
Решение 2:   Построим треугольник YB₂C₂, подобный треугольнику ABC и лежащий с ним в разных полуплоскостях относительно BC (рис. справа). Так как

B₂C₂ = ½ BC,  точки B₃, Y и C₃ находятся на одном и том же расстоянии от BC (равном половине расстояния от A до BC). Кроме того,

YB₂ = ½ AB = BB₃  и  YC₂ = ½ AC = CC₃.  Значит, BB₂YB₃ и CC₂YC₃ – равнобокие трапеции, и Y – одна из общих точек описанных окружностей треугольников BB₂B₃ и CC₂C₃.

  Так как степени точки A₁ относительно этих окружностей равны, вторая точка их пересечения лежит на прямой A₁Y. Пусть луч A₁Y пересекает описанную около ABC окружность в точке X. Так как AA₁ и YA₁ – соответственные медианы в подобных треугольниках ABC и YB₂C₂, получаем

∠XA₁C = ∠CA₁A,  а значит, как и в решении 1,  A₁X<·A₁A = A₁B·A₁C.  Поэтому A₁X·A₁Y = ½ A₁X·A₁A = ½ A₁B² = A₁B·A₁B₂,  то есть X и есть вторая точка пересечения окружностей.

Ответ задачи отсутствует