Задача
Докажите, что всякий треугольник площади 1 можно накрыть равнобедренным треугольником площади менее 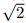 .
.
Решение
Пусть ABC – данный треугольник (AB ≥ AC ≥ BC), CH – его высота, точка A' симметрична A относительно H, а точка B' симметрична B
относительно биссектрисы угла A (см. рис.). Тогда ACA' и ABB' – равнобедренные треугольники, накрывающие ABC, причём 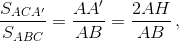 а
а 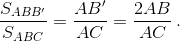 Произведение этих отношений есть 2AH/AC < 2, значит, какое-то из них меньше
Произведение этих отношений есть 2AH/AC < 2, значит, какое-то из них меньше 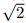 .
.
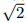
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет