Все углы в решении предполагаются ориентированными.

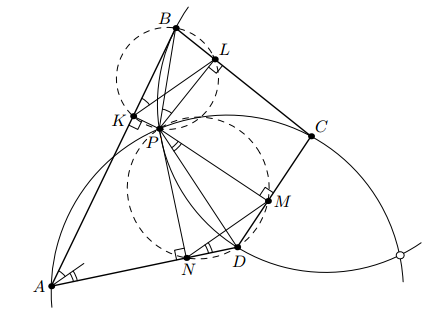
  Пусть K, L, M и N – проекции искомой точки P на стороны AB, BC, CD и DA соответственно. Условие  KL || MN  равносильно тому, что

∠BKL + ∠MND = ∠BAD.  В силу вписанности четырёхугольников PKBL и PMDN имеем  ∠BKL = ∠BPL  и  ∠MND = ∠MPD.  Следовательно, условие  KL || MN  равносильно тому, что  ∠BPD = ∠BPL + ∠MPD + ∠LPM = ∠BAD + (180° – ∠DCB).

  Значит, мы можем построить окружность, проходящую через B и D, на которой лежит точка P (см. рис.).

  Аналогично условие  KN || LM  равносильно тому, что  ∠CPA = 180° + ∠CBA – ∠ADC,  и можно построить окружность, проходящую через A и C и содержащую P. Одной из точек пересечения полученных двух окружностей будет точка Микеля четвёрки прямых AB, BC, CD и DA (её проекции на стороны четырёхугольника лежат на одной прямой; см. задачи 156628 и 156632). Вторая точка пересечения – искомая.

Ответ задачи отсутствует