Пусть ABCD – данный четырёхугольник. Если  AB + CD = AD + BC,  то в него можно вписать окружность. Радиусы этой окружности, проведённые в точки касания со сторонами, разрезают четырёхугольник на четыре симметричных четырёхугольника. Разрезав затем один из этих четырёхугольников на два равнобедренных треугольника, получим искомое разрезание.

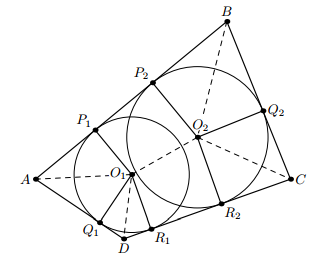
  Пусть  AB + CD > AD + BC.  Построим окружность с центром O₁, касающуюся сторон AB, AD и CD в точках P₁, Q₁ и R₁ соответственно, и окружность с центром O₂, касающуюся AB, BC и CD в точках P₂, Q₂ и R₂. Радиусы, проведённые в эти точки, разрезают ABCD на четырёхугольники AP₁O₁Q₁, BP₂O₂Q₂, CQ₂O₂R₂, DQ₁O₁R₁ и шестиугольник P₁P₂O₂R₂R₁O₁, симметричные относительно биссектрис углов A, B, C, D и биссектрисы угла между прямыми AB и CD соответственно.

Ответ задачи отсутствует