Решение 1:Пусть K – такая точка на стороне CD, что  CK = CB,  M – точка пересечения AB с перпендикуляром, восставленным из точки K к прямой CD. Тогда прямоугольные треугольники BCM и KCM равны по катету и гипотенузе, то есть  BM = MK,  а CM – биссектриса угла C. Кроме того, из условия следует, что  KD = AD,  откуда аналогично  AM = MK,  а DM – биссектриса угла D. Поэтому  AM = ½ AB = AE,  и, значит, равны треугольники ABE и ADM. Следовательно,  ∠ADC = 2∠ADM = 2∠ABE  (см. рис.).

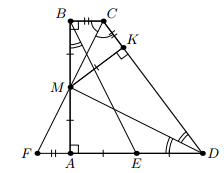
Решение 2:Отложим на продолжении DA за точку A отрезок  AF = BC,  тогда  DF = DC.  Пусть M – точка пересечения AB и CF, то есть середина AB. Прямоугольные треугольники ABE и ADM равны, DM – медиана равнобедренного треугольника CDF, поэтому она – биссектриса угла CDA, то есть

½ ∠CDA = ∠ABE.

Ответ задачи отсутствует