Задача
Если один человек тратит в очереди одну минуту на ожидание, будем говорить, что бесцельно затрачена одна человеко-минута. В очереди в банке стоит восемь человек, из них пятеро планируют простые операции, занимающие 1 минуту, а остальные планируют длительные операции, занимающие 5 минут. Найдите:
а) наименьшее и наибольшее возможное суммарное количество бесцельно затраченных человеко-минут;
б) математическое ожидание количества бесцельно затраченных человеко-минут, при условии, что клиенты встают в очередь в случайном порядке.
Решение
Пусть короткая операция занимает a, а длинная – b минут (a < b). Клиента, планирующего простую операцию, будем называть торопыгой, а того, кто собирается возиться долго – копушей. Предположим, что торопыг всего n, а копуш – m.
Очевидно, число бесцельно потраченных человеко-минут зависит от порядка, в котором чередуются торопыги и копуши. а) Пусть где-то в очереди торопыга стоит сразу за копушей. Поменяем их местами. Тогда
те, кто стоит перед ними ничего не выигрывают и не проигрывают;
для тех, кто за ними, время ожидания также не меняется;
для торопыги время ожидания уменьшается на b минут.
для копуши время ожидания увеличится на a минут.
Следовательно, суммарное бесцельно потраченное время всех стоящих в очереди, уменьшится на b – a минут. Будем таким образом переставлять местами людей в парах "копуша-торопыга" до тех пор, пока не получится очередь, в которой все торопыги стоят прежде всех копуш. В этой очереди бесцельно потраченное время будет минимальным.
Найдём суммарное бесцельно потраченное время. Второй человек ждет первого, третий ждет предыдущих двух и так далее.
Суммарное время, которое тратят ждущие, пока все впереди стоящие торопыги не закончат свои операции, равно
(a + 2a + ... + (n – 1)a) + mna = ½ an(n – 1) + mna.
Здесь слагаемое mna – это суммарное время, потраченное всеми копушами на ожидание всех торопыг.
Суммарное время, которое тратят ждущие, пока свои операции проводят впереди стоящие копуши, равно (b + 2b + ... + (m – 1)b) = ½ bm(m – 1). Общее минимальное время ожидания всеми клиентами равно Tmin = ½ an(n – 1) + mna + ½ bm(m – 1). В нашем конкретном случае получаем: 1·10 + 1·3·5 + 5·3 = 40.
Аналогично доказывается, что наибольшее бесцельно потраченное время будет, если все копуши стоят прежде всех торопыг. Это время равно
Tmax = ½ an(n – 1) + mnb + ½ bm(m – 1).
При числовых данных задачи получается 1·10 + 5·3·5 + 5·3 = 100. б) Рассмотрим k-го клиента в очереди. Обозначим через Xk число копуш, стоящих перед ним. Тогда Xk = I1 + I2 + ... + Ik–1, где индикатор Ij принимает значение 1, если j-й клиент – копуша и 0, если j-й клиент – торопыга. j-й клиент может оказаться копушей с вероятностью m/m+n и торопыгой с вероятностью n/m+n. Значит, EIj = m/m+n.
Следовательно, 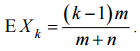
Обозначим через Tk время ожидания k-го клиента. Получаем: Tk = Xkb + (k – 1 – Xk)a = (b – a)Xk + a(k – 1).
Следовательно, 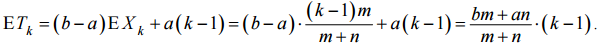
Суммируя по всем клиентам от первого до (m+n)-го, получаем математическое ожидание всего бесцельно затраченного времени:

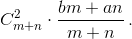
Подставим известные из условия числа: 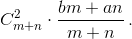
Ответ
а) 40 минут и 100 минут; б) 70 минут.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь