а) Пронумеруем пары от 1 до N (мы не знаем, сколько их) в том порядке, в каком они лежат на столе. Пусть индикатор I_k равен 1, если в k-й паре оказались две одинаковые карты, и 0, если в k-й паре карты не одинаковы. Очевидно,  P(I_k = 1) = ¹/_N.  Значит,  EI_k = ¹/_N.

  Пусть S – число пар с совпадением. Оно равно  I₁ + I₂ + ... + I_N.  Следовательно,  ES = EI₁ + EI₂

• ... + EI_N = N·¹/_N = 1.   б) 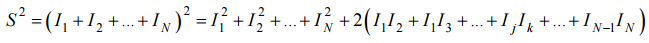 ,  где в скобках стоит сумма попарных произведений всевозможных различных индикаторов.

  Очевидно, 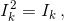   поэтому  .

  Теперь рассмотрим величину I_jI_k. Она равна 1, если карты совпали и в j-й, и в k-й паре. В j-й паре карты совпадают с вероятностью ¹/_N. Если это произошло, то вероятность совпадения карт в k-й паре равна ¹/_N–1. Поэтому  P(I_jI_k = 1) = ¹/_N(N–1)  Во всех остальных случаях I_jI_k = 0. Следовательно,  E(I_jI_k) = ¹/_N(N–1).

 Значит,  ES² = N·¹/_N + N(N – 1)·¹/_N(N–1) = 1 + 1 = 2,  и, следовательно,  DS = ES² – (ES)² = 2 – 1 = 1.

а) 1;  б) 1.