Задача
Бросим симметричную монету n раз. Предположим, что орёл выпал m раз. Число m/n называется частотой выпадения орла. Число m/n – 0,5 называется отклонением частоты от вероятности, а число |m/n – 0,5| называется абсолютным отклонением. Заметим, что отклонение и абсолютное отклонение являются случайными величинами. Например, если монету бросили 5 раз, и два раза выпал орёл, то отклонение равно ⅖ – 0,5 = –0,1, а абсолютное отклонение равно 0,1.
Эксперимент состоит из двух частей: сначала монету бросают 10 раз, а потом – 100 раз. В каком из этих случаев больше математическое ожидание абсолютного отклонения частоты выпадения орла от вероятности?
Решение
Пусть в серии из 10 бросаний орёл выпал m раз. Тогда отклонение частоты от вероятности равно |α|, где α = m/10 – 0,5.
Вторую последовательность, состоящую из 100 бросаний, разобьём на 10 серий по десять бросков. В каждой из этих 10 малых серий имеется своё отклонение (неабсолютное) αi (i – номер серии), причём E|αi| = E|α|.
Тогда отклонение β в последовательности 100 бросаний равно 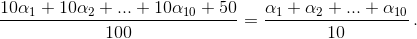
Ответ
В серии из 10 бросков.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь