Задача
В страшную грозу по верёвочной лестнице цепочкой поднимаются n гномиков. Если вдруг случится удар грома, то от испуга каждый гномик, независимо от других, может упасть с вероятностью p (0 < p < 1). Если гномик падает, то он сшибает и всех гномиков, которые находятся ниже. Найдите:
а) Вероятность того, что упадёт ровно k гномиков.
б) Математическое ожидание числа упавших гномиков.
Решение
Пусть q = 1 – p – вероятность того, что гномик не упадёт от испуга (хотя, может быть, упадёт, но не от испуга, а от того, что на него кто-то свалился сверху). а) Ровноkгномиков упадёт, только если упадёт от испугаk-й гномик, считая снизу, и не упадёт ни один из n – k гномиков, находящихся выше. Значит, искомая вероятность равна pqn–k = p(1 –p)n–k. б) Используеминдикаторы. Пусть случайная величинаIjравна 1, еслиj-й гномик падает и 0, если он не падает. Вероятность того, чтоj-й гномик не упадёт, равна вероятности того, не упадёт он сам и не упадёт никто из j– 1 гномиков, расположенных выше: P(Ij= 0) =qj. Следовательно, EIj=P(Ij= 1) = 1 –q. Общее числа упавших гномиков равно сумме всех индикаторов, значит, ожидание этой величины равно
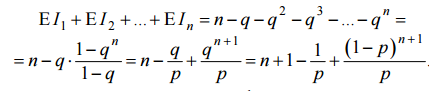
Ответ
а) p(1 – p)n–k; б) 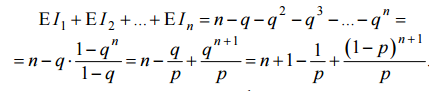 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь