Задача
Найдите вероятность того, что орёл выпадет чётное число раз, в эксперименте, в котором:
а) симметричную монету бросают n раз;
б) n раз бросают монету, у которой вероятность выпадения орла при одном бросании равна p (0 < p < 1).
Решение
Вероятность того, что орёл выпадет ровно k раз, как известно, равна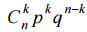 
,
где q = 1 – p – вероятность выпадения решки. Поэтому событие "Орёл выпал чётное число раз" имеет вероятность 
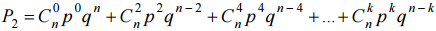, где
k – наибольшее чётное число, не превосходящее n.
Дополнением к этому событию служит событие "Орёл выпал нечётное число раз". Вероятность этого получается аналогично заменой чётных индексов и
степеней нечётными: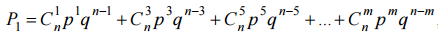 
, где m – наибольшее нечётное, не превосходящее n. Разность этих вероятностей: 
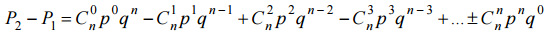= (q – p)n.
С другой стороны, P2 + P1 = 1. Из полученной системы уравнений находим:
.
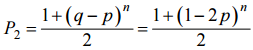В частности, для симметричной монеты p = 0,5, поэтому P2 = 0,5.
Ответ
а) 0,5; б)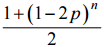 
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь