Задача
На рисунке показано платежное поручение на оплату электричества некоторой энергосбытовой компании.
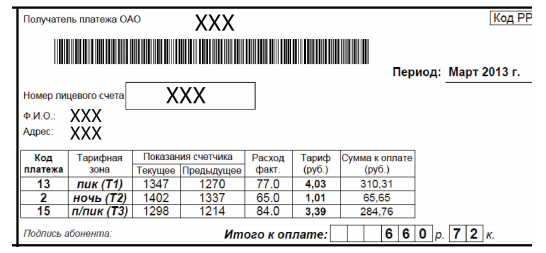
Компания ведет учёт расхода и оплаты электроэнергии, пользуясь данными, полученными от клиента. Проблема состоит в том, что компания иногда путает полученные шесть чисел, переставляя их произвольном порядке, правда, следит за тем, чтобы текущее показание оставалось больше, чем предыдущее. В результате расчёт компании может оказаться ошибочным. Если компания считает, что клиент должен больше, чем он заплатил, компания требует доплатить разность.
Пользуясь данными изображенной квитанции, найдите:
а) максимально возможную сумму доплаты за март 2013 года, которую компания потребует у клиента;
б) математическое ожидание разности между суммой, которую насчитает компания, и суммой, которую заплатил клиент.
Решение
а) Очевидно, что сумма, которую потребует компания, будет наибольшей, если расход по самому высокому тарифу будет наибольшим возможным, по среднему – наибольшим возможным из оставшихся. Наибольшая возможная сумма при этом равна 4,03·(1402 – 1214) + 3,39·(1347 – 1270) + 1,01·(1337 – 1298) = 1058,06 (руб.). Компания потребует доплатить 1058,06 – 660,72 = 397,34 (руб.). б) Решим задачу в общем виде, считая, что клиент передал шесть различных чисел a < b < c < d < e < f. Рассмотрим одну из тарифных зон (например, пик). Для этой зоны можно выбрать два любых числа из данных шести и поставить их в соответствующем порядке – по возрастанию. Это можно сделать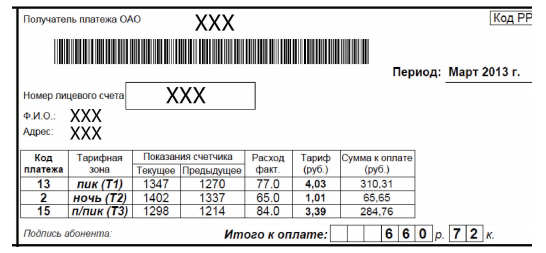 
способами. По условию все способы равновозможны. Поэтому математическое ожидание EX1 случайной величины X1 "Расход по тарифу Пик" есть среднее арифметическое
пятнадцати чисел: f – e, f – d, f – c, f – b, f – a, e – d, e – c, e – b, e – a, d – c, d – b, d – a,
c – b, c – a, b – a, то есть EX1 = 1/15 (5f + 3e + d – c – 3b – 5a).
Очевидно, такое же ожидание имеют случайные величины X2 и X3 "Расход по тарифу Ночь" и "Расход по тарифу Полупик". Полная сумма оплаты S, рассчитанная компанией, равна t1X1 + t2X2 + t3X3, где t1, t2 и t3 – цены одного киловатт-часа по соответствующим тарифам. Следовательно,
ES = t1EX1 + t2EX2 + t3EX3 = 1/15 (5f + 3e + d – c – 3b – 5a)(t1 + t2 + t3).
В нашем случае f = 1402, e = 1347, d = 1337, c = 1298, b = 1270, a = 1214; t1 + t2 + t3 = 4,03 + 1,01 + 3,39 = 8,43. Таким образом,
ES = 1/15 (5·1402 + 3·1347 + 1337 – 1298 – 3·1270 – 5·1214)·8,43 = 1210/15·8,43 = 680,02.
Математическое ожидание разности между суммой, которую потребует сбытовая компания и суммой, которую заплатит клиент, равно
ES – 660,72 = 680,02 – 660,72 = 19,03 (руб.)
Ответ
а) 397 руб. 34 коп.; б) 19 руб. 3 коп.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь