Задача
Будем считать, что рождение девочки и мальчика равновероятны. Известно, что в некоторой семье двое детей.
а) Какова вероятность того, что из них один мальчик и одна девочка?
б) Дополнительно известно, что один из детей – мальчик. Какова теперь вероятность того, что в семье один мальчик и одна девочка?
в) Дополнительно известно, что мальчик родился в понедельник. Какова теперь вероятность того, что в семье один мальчик и одна девочка?
Решение
а) Дети появляются в некоторой последовательности (ММ, МД, ДМ или ДД). Все последовательности равновозможны, и вероятность каждой ¼. Условию "Мальчик и девочка" благоприятствуют два исхода МД и ДМ, значит, вероятность этого равна 2 : 4 = ½. б) Из четырёх последовательностей остаются три равновозможных: ММ, МД и ДМ. Следовательно, теперь вероятность события "мальчик и девочка" равна ⅔. в) Введём дополнительно в рассмотрение дни недели: МП – мальчик, родившийся в понедельник, МИ – мальчик, родившийся в другой день недели. По условию возможны пять последовательностей: МПМП, МПМИ, МИМП, МПД, ДМП.
Учитывая, что вероятность родиться в понедельник равна 1/7, а в другой день – 6/7, находим, что суммарная вероятность возможных последовательностей равна 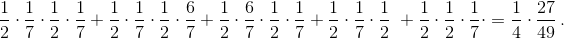
Из этих последовательностей только две: МПД и ДМП благоприятствуют событию "мальчик и девочка". Их суммарная вероятность равна ¼·2/7.
Следовательно, условная вероятность события "мальчик и девочка" при условии "есть мальчик, родившийся в понедельник" равна 2/7 : 27/49 = 14/27.
Ответ
а) ½; б) ⅔; в) 14/27.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь