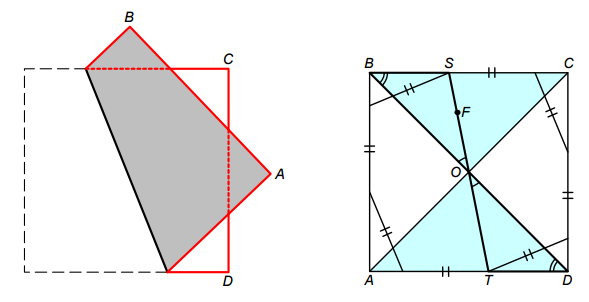
Развернём красивый сгиб (рис. справа). Пусть диагональ BD и линия сгиба ST пересекаются в точке O. Треугольники BSO и DTO равны по стороне и двум углам. Значит,  BO = OD,  и поэтому O – центр квадрата. Таким образом, линия сгиба ST проходит через центр квадрата. Очевидно, обратное также верно – если линия сгиба проходит через центр квадрата, то сгиб будет красивым.

  ТочкаSможет занять любое положение междуBиC, а точкаTпри этом расположена междуDиA. Значит, чтобы через точкуFможно было сделать красивый сгиб, нужно, чтобы точкаFпринадлежала треугольникуBOCили треугольникуAOD.   Площадь фигуры, ограниченной этими треугольниками, равна половине площади квадрата.

½.