Задача
Правильная игральная кость бросается много раз. Известно, что в какой-то момент сумма очков стала равна ровно 2010.
Найдите математическое ожидание числа бросков, сделанных к этому моменту.
Решение
Первый способ. Пусть событие An "сумма очков равна n , а Xn – число сделанных при этом бросков. Событие An мы считаем уже осуществившимся, и нас интересует ожидание EXn. Пусть Ik равно 1, если первый бросок дал k очков, и 0 в противном случае.
События Bk "первый бросок дал k очков" и An–k (для оставшихся бросков) относятся к разным броскам и поэтому независимы. Следовательно, условная вероятность события (Ik = 1) равна   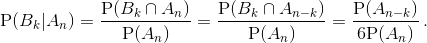
Ясно, что Xn = Xn–1I1 + Xn–2I2 + ... + Xn–6I6 + 1.
При этом случайные величины Xn–k и Ik независимы, поскольку относятся к разным сериям бросков. Поэтому 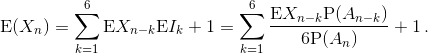
Вводя обозначения EXk = ek и P(Ak) = pk, получаем: 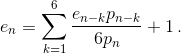 (1)
(1)
Осталось воспользоваться тем, что 6pn = pn–1 + ... + pn–6. Это следует, например, из того, что сумма вероятностей P(Ik = 1) равна единице. Значит, 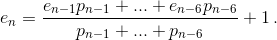
Начальные значения: p–5 = p–4 = ... = p–1 = 0; p0 = 1; e–5 = e–4 = ... = e0 = 0. Последовательное вычисление дает e1 = 1, p1 = 1/6;
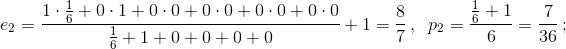
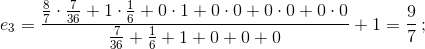 ...,
...,
e2010 = 574,5238095... Второй способ. Известно, что сумма очков сравнялась с n. Пусть наступило событие Ak "в какой-то момент сумма равна k". Тогда последующие броски должны привести к событию An–k. Значит, 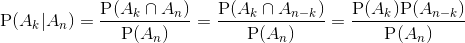 (cобытия An–k и Ak относятся к разным сериям бросков и поэтому независимы).
(cобытия An–k и Ak относятся к разным сериям бросков и поэтому независимы).
Рассмотрим величину Jk, которая равна 1, если сумма в какой-то момент равна k, и 0 в противном случае.
Очевидно, случайная величина "число полученных сумм" Xn = J1 + J2 + ... + Jn равна числу сделанных бросков.
Введём краткие обозначения EXk = ek, P(Ak) = pk. Математическое ожидание EJk равно 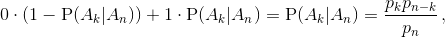 следовательно,
следовательно, 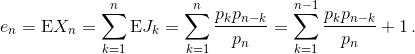
Пользуясь соотношением pn–k = 1/6 (pn–k–1 + ... + pn–k–6), запишем ожидание иначе:
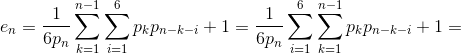
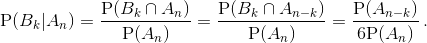
Ответ
574,5238095...
Чтобы оставлять комментарии, войдите или зарегистрируйтесь