Задача
В бумажном квадрате случайным образом выбирается точка O. Затем квадрат сгибают так, чтобы каждая вершина наложилась на точку O. На рисунке показана одна из возможных схем складывания. Найдите математическое ожидание числа сторон появившегося многоугольника.
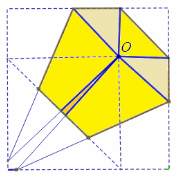
Решение
Небольшое геометрическое исследование показывает, что в результате может получиться шестиугольник, пятиугольник и четырёхугольник. Четырёхугольник получается, только если точка O попала точно в центр или в вершину квадрата. Вероятность этого равна нулю.
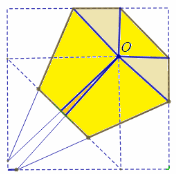
Ответ
4 + π/2 ≈ 5,571.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет