Задача
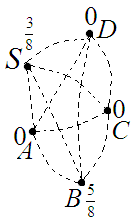
В Долине Пяти Озёр есть пять одинаковых озёр, некоторые из которых соединены ручьями (на рис. пунктиром обозначены возможные "маршруты" ручьёв). Маленькие караси появляются на свет только в озере S. Пока карась взрослеет, он ровно четыре раз переходит из одного озера в другое по какому-нибудь ручью (карась выбирает ручей наудачу), а затем остается жить в том озере, в котором оказался. Из каждой тысячи карасей в среднем 375 остается жить в озере S, а остальные остаются жить в озере B, в других озерах не остается жить никто. Определите, сколько ручьёв в Долине Пяти Озёр.
Решение
Переход из озера в озеро будем называть маршрутом длины n, если он проходит через n ручьев. Докажем несколько утверждений. 1. Из S нет маршрута длины 2 ни в одно из озер A, C и D.
Доказательство. Предположим, что из озера S можно проплыть в озеро A через одно промежуточное озеро (скажем C). Тогда был бы возможен маршрут S – C – A – C – A. В этом случае, была бы ненулевая вероятность попасть в озеро A за четыре перехода. Значит из S в A маршрута длины 2 нет.
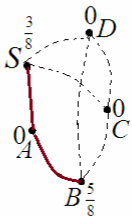
Доказательство. Очевидно, S и B связаны. Предположим, они связаны общим ручьем. Тогда из B нет других выходов, иначе не выполнено условие (1). Значит, в можно прийти только из S на первом или третьем ходу. Но тогда после четвёртого перехода попасть в B карась не сможет. Противоречие.
Предположим, что S и B связаны маршрутом длины 3 или 4. Но тогда есть маршрут длины 2 из S в одно из озёр A, C или D, а его быть не может.
Значит, из S в B есть маршрут, проходящий через одно промежуточное озеро A, C или D, причём одно ничем не хуже другого. Можно для определенности считать, что есть маршрут S – A – B.
Из этого и утверждения 1 следует, что нет маршрутов A – C и A – D. 3. Есть хотя бы один из маршрутов B – C или B – D.
Доказательство. Предположим, что нет ни маршрута B – C, ни B – D. Получаем один из следующих рисунков.
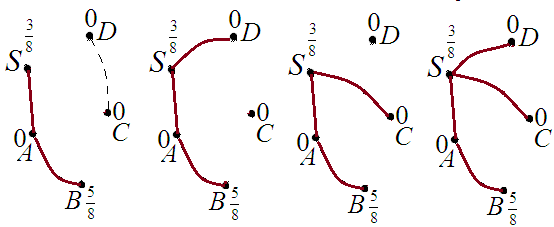
Доказательство. Для построенной конфигурации возможны следующие маршруты длины 4:
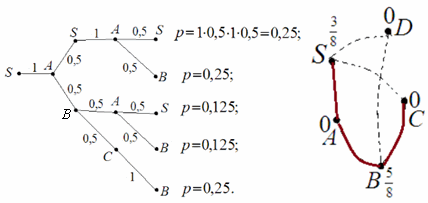
Доказательство. Добавляя любые ручьи S – C, S – D, B – D порознь или вместе, мы изменим вероятности. В этом можно убедиться непосредственно, сделав еще семь рисунков, соответствующих возможным конфигурациям и рассчитав вероятности для каждой из полученных схем. Таким образом, с точностью до обозначения вершин, схема, показанная на последнем рисунке – единственно возможная, а общее число ручьёв равно 3.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь