Задача
На улице n домов. Каждый день почтальон идёт на почту, берёт там письма для жителей одного дома и разносит их. Затем он возвращается на почту, берёт письма для жителей другого дома и снова их разносит. И так он обходит все дома. В каком месте нужно построить почту, чтобы почтальону пришлось проходить наименьшее расстояние? Улицу можно считать отрезком прямой.
а) Решите задачу для n = 5.
б) Решите задачу для n = 6.
в) Решите задачу для произвольного n.
Решение
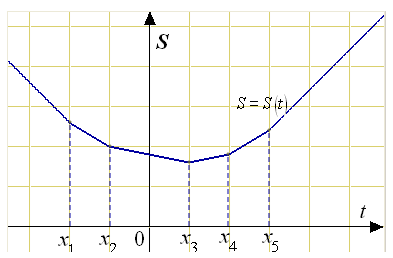
а) Введём координатную прямую, на которой расположим дома с координатами x1, x2, x3, x4, x5 упорядоченными по возрастанию. Пусть t – координата почтового отделения на числовой прямой.

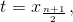 а при чётных n минимум достигается на всем отрезке
а при чётных n минимум достигается на всем отрезке 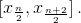
Ответ
а) В среднем доме; б) в любой точке отрезка между двумя средними домами;
в) при нечётном n в среднем доме, при чётном – в любой точке отрезка между двумя средними домами.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь