Задача
Верхняя сторона бумажного квадрата белая, а нижняя – красная. В квадрате случайным образом выбирается точка F. Затем квадрат сгибают так, чтобы одна случайно выбранная вершина наложилась на точку F. Найдите математическое ожидание числа сторон появившегося красного многоугольника.
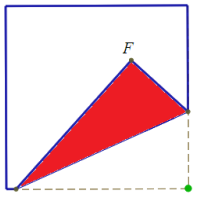
Решение
Результат зависит только от взаимного положения точки F и выбранной вершины. Поэтому можно считать, что вершина фиксирована (пусть это будет вершина A), а точка F выбирается случайно.
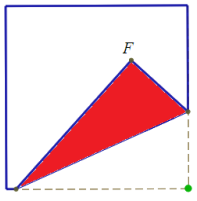
Ответ
5 – π/2 ≈ 3,429.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет