Задача
Вася в ярости режет прямоугольный лист бумаги ножницами. Каждую секунду он разрезает первый попавшийся кусок случайным прямолинейным разрезом на две части.
а) Найдите математическое ожидание числа сторон многоугольника, который случайно попадётся Васе через час такой работы.
б) Решите эту же задачу, если вначале лист бумаги имел форму произвольного многоугольника.
Решение
б) Пусть в результате Васиной деятельности на столе оказался k + 1 многоугольник, в том числе p3 треугольников, p4 четырёхугольников, ..., pm m-угольников (m – наибольшее возможное число сторон у получившегося многоугольника). Тогда математическое ожидание числа сторон выбранного многоугольника равно 1/k+1 (3p3 + 4p4 + ... + mpm).
В скобках находится общее число сторон всех полученных многоугольников.
Предположим, что у Васи был n-угольник. Вероятность сделать случайный разрез точно через какую-нибудь вершину равна нулю. Значит, каждый разрез делит какие-то две стороны разрезаемого многоугольника на две части каждую, и еще две новые стороны получаются вдоль разреза. Таким образом, каждый разрез добавляет 4 новые стороны. После k разрезов общее число сторон будет равно n + 4k.
Таким образом, 
. а) Если вначале у Васи был четырёхугольник, то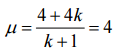 
.
Ответ
а) 4; б)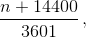 
где n – число сторон исходного многоугольника.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь