Задача
Дан числовой набор x1, ..., xn. Рассмотрим функцию 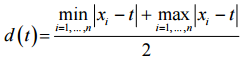 .
.
а) Верно ли, что функция d(t) принимает наименьшее значение в единственной точке, каков бы ни был набор чисел x1, ..., xn?
б) Сравните значения d(c) и d(m), где
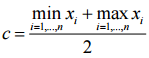 , а m
– медиана указанного набора.
, а m
– медиана указанного набора.
Решение
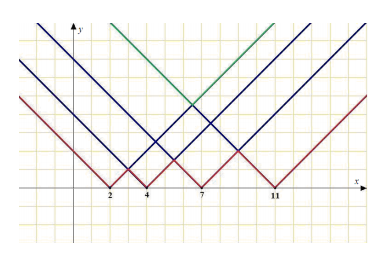
а) Рассмотрим набор {2, 4, 7, 11}. Построим функцию d(t) для этого набора. Сначала построим графики функций y = |x – 2|, y = |x – 4|, y = |x – 7|, y = |x – 11|.
Теперь построим графики функции 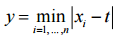 (красный) и
(красный) и 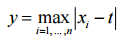 (зелёный).
(зелёный).
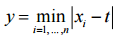 . При этом функция y = d(t), очевидно, не может возрастать там, где убывает функция
. При этом функция y = d(t), очевидно, не может возрастать там, где убывает функция 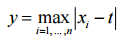 и не может убывать там, где эта функция возрастает.
и не может убывать там, где эта функция возрастает.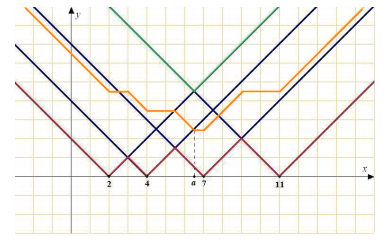
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет