Задача
Учительница математики предложила изменить схему голосования на конкурсе спектаклей (см. задачу 165299). По её мнению, нужно из всех 2n мам выбрать случайным образом жюри из 2m человек (2m ≤ n). Найдите вероятность того, что лучший спектакль победит при таких условиях голосования.
Решение
Назовём маму честной, если она голосует за лучший спектакль. Поскольку всего нечестных мамnи столько же честных, вероятность того, что в жюри попалоqнечестных мам и 2m
– q честных, равна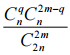 .
Если это событие осуществилось, то судьба конкурса зависит от
распределения голосов нечестных мам. Еслиtдетей нечестных мам играет в худшем спектакле, то этот худший спектакль получит ровноtголосов, тогда как все прочие голоса числом 2m – t будут отданы лучшему спектаклю. Таким образом, лучший спектакль побеждает, если 2m – t > t, то есть если t < m.
Вероятность того, что худший спектакль получит ровноtголосов, равна вероятности
.
Если это событие осуществилось, то судьба конкурса зависит от
распределения голосов нечестных мам. Еслиtдетей нечестных мам играет в худшем спектакле, то этот худший спектакль получит ровноtголосов, тогда как все прочие голоса числом 2m – t будут отданы лучшему спектаклю. Таким образом, лучший спектакль побеждает, если 2m – t > t, то есть если t < m.
Вероятность того, что худший спектакль получит ровноtголосов, равна вероятности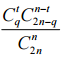 того, что ровноtдетей нечестных мам из жюри играет в этом спектакле.
Следовательно, вероятность комбинации, при которой в жюри собираетсяqнечестных мам, и худший спектакль получает меньше голосов, чем
лучший, равна
того, что ровноtдетей нечестных мам из жюри играет в этом спектакле.
Следовательно, вероятность комбинации, при которой в жюри собираетсяqнечестных мам, и худший спектакль получает меньше голосов, чем
лучший, равна 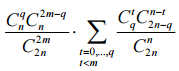 .
Суммируя эти вероятности по всем возможным распределениям нечестных мам,
получаем, что искомая вероятность равна
.
Суммируя эти вероятности по всем возможным распределениям нечестных мам,
получаем, что искомая вероятность равна
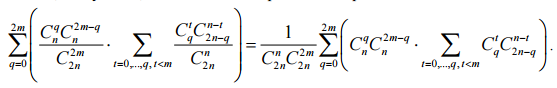
Ответ
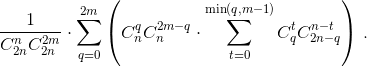
Чтобы оставлять комментарии, войдите или зарегистрируйтесь