Задача
В финал конкурса спектаклей к 8 Марта вышли два спектакля. В первом играли n учеников 5 класса А, а во втором – n учеников 5 класса Б. На спектакле присутствовали 2n мам всех 2n учеников. Лучший спектакль выбирается голосованием мам. Известно, что ровно половина мам честно голосует за лучший спектакль, а другая половина в любом случае голосует за спектакль, в котором участвует её ребенок.
а) Найдите вероятность того, что лучший спектакль победит с перевесом голосов. б) Тот же вопрос, если в финал вышло больше двух спектаклей.
Решение
а) Назовём маму честной, если она в любом случае голосует за лучший спектакль. Известно, что n честных мам будет голосовать за лучший спектакль, поэтому он заведомо не проиграет (половина голосов точно за него). Единственный случай, когда лучший спектакль не победит – ничья, когда худший спектакль также наберет половину голосов. Это возможно только если все дети нечестных мам играют в худшем спектакле. Найдем вероятность этого события.
Всего существует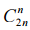 
случаев распределения n нечестных мам среди общего числа 2n мам. И только в одном из этих случаев все нечестные мамы голосуют за худший спектакль. Таким образом, вероятность ничьей равна 
.
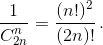Следовательно, вероятность события "лучший спектакль наберёт больше голосов" равна 
= 
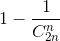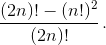б) Пусть спектаклей m > 2. В этом случае лучший спектакль побеждает наверняка – он получает, по крайней мере, половину голосов по одному от каждой честной мамы. Голоса остальных мам делятся между прочими спектаклями, каждый из которых получает не более, чем 1/m всех голосов, что меньше половины.
Ответ
а) 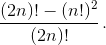б) 1.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь